Analyses for surveys designed with stratification and clustering
Survey weights are calculated to estimate the probability of selected households and individuals being included in the survey sample compared with the probability of each household or individual in the entire population being included in the survey sample. These survey weights are then used in the analysis to adjust the survey data to represent the larger sampling frame of households that all have an equal probability of being sampled.
Weighting for stratification
A stratified sample is produced when the population is divided into distinct, independent strata. Using PPS to select PSUs followed by systematic random sampling of an equal number of households within clusters means that each household within the stratum has an equal probability of being selected. This is described in more detail in Module 4: Survey Design; Module 5: Sample Size; and Module 6: Selecting Clusters.
Stratum-level data can be used to produce nationally representative estimates by adjustment or weighting for the proportion of the national population in each stratum. Table 15.1 shows an example of calculating stratum weights, where regions A, B and C represent survey strata. The respective populations are indicated in two ways: as numbers and as percentages of the national population. The number of specimens tested for haemoglobin is also stated, along with the proportion of the total test specimens within each stratum.
Table 15.1. Example of calculating stratum weights for use in analysis of estimates based on haemoglobin samples
Region
(stratum)Population Haemoglobin specimens tested Stratum weight Ia Stratum weight IIb n % n % A 372 978 62.9 334 34.5 1116.70 1.823 B 127 841 21.6 324 33.5 394.57 0.645 B 127 841 21.6 324 33.5 394.57 0.645 C 92 117 15.5 309 32.0 298.11 0.484 Total 592 936 100.0 967 100.0 – a Column 1 divided by column 3
b Column 2 divided by column 4
To derive a correct national estimate based on haemoglobin specimens, stratum weights need to be applied to each stratum to account for differences in population size. There are two approaches for calculating the stratum-specific weights. Table 15.1 describes them as “stratum weight I” and “stratum weight II” to differentiate the two methods. Whichever method is used, it must be applied consistently for all survey data.
The calculation of stratum weight I requires the approximate number of individuals that each survey sample represents. This is determined by dividing the population number in the stratum by the number of participants sampled in that stratum. In Table 15.1, the stratum weight I for Region A is 372 978 ÷ 334 = 1116.70. In other words, every individual sampled for haemoglobin can be considered to be representative of 1116.70 individuals in the region.
The calculation of stratum weight II requires dividing the percentage of the population in each stratum by the percentage of the specimens collected in each stratum. In Table 15.1, the stratum weight II for Region A is 62.9 ÷ 34.5 = 1.823. This alternate approach can be useful when the total population size per region is not available, for example if a census has not been updated or if there is conflicting information between the census and other reliable estimates of population size.
Once the stratum weights are calculated, they should be added to the data file. In the example shown in Table 15.1, if the method for stratum weight II were used, then each individual sampled from Region A would have the weight 1.823, each individual sampled in Region B would have the weight 0.645 and each individual sampled in Region C would have the weight 0.484.
Depending on the survey sampling design and factors affecting non-response and missing data, different weights may need to be calculated for different variables. More information on adjusting sampling weights for non-response or missing data can be found in the Feed the Future Population-Based Survey Sampling Guide. 1
Important considerations related to clustering
As described in Module 5: Sample Size, the design effect (DEFF) and intra-cluster correlation (ICC) are important indicators of the effect that using a cluster survey has on the data, when compared with a survey based on SRS. Both the DEFF and ICC can be estimated from the data during the analysis phase of the survey. The DEFF is equal to the variance accounting for the complex survey design, divided by the variance assuming SRS.
The following sections focus on analysis of data from cluster surveys that used the PPS approach to selecting PSUs.
Calculating percentages for stratified cluster data
Calculating percentages for stratified cluster survey data is very similar to calculating percentages for data collected using SRS, with the exception that a stratum weight variable is included in the calculation. Table 15.2 presents the number of individuals with haemoglobin samples who were found to be anaemic along with the unweighted percent prevalence for each stratum.
Table 15.2. Example of calculating stratum weights for use in analysis of estimates based on haemoglobin samples
Region (stratum) Population Haemoglobin specimens tested Specimens categorized as low haemoglobin (anaemia) Unweighted survey result for anaemia n % n % n % A 372 978 62.98 334 34.5 112 33.5 B 127 841 21.6 324 33.5 185 57.1 C 92 117 15.5 309 32.0 119 38.5 Total 592 936 100.0 967> 100.0 416 43.0a, a The national percent estimate here is unweighted and incorrect, see text below.
Samples within a stratum are generally self-weighted, assuming PPS selection of PSUs and systematic selection of households and individuals within households within the cluster, with similar non-random non-response between clusters. Therefore, the unweighted prevalence of anaemia for each of the three regions is likely to be fairly reliable, unless there was a significantly different pattern of non-response or missing values between clusters within a stratum
An incorrect approach to obtaining the national estimate for anaemia prevalence would be to add the total number of people with anaemia (416), and divide this by the total number of samples tested (967), and then multiply by 100 to obtain the percentage (416 ÷ 967) x 100 = 43.0%. This unweighted percentage gives the percentage of tested samples with low haemoglobin but does not provide a correct estimate of the percentage of the national population with low haemoglobin. The unweighted estimate ignores the fact that the population size in Stratum B is about one third as large as the population in Stratum A and about 1.4 times larger than in Stratum C.
The calculation to determine the correct weighted prevalence of anaemia among the population must take into consideration the population size in each region. For this example, the correct population estimate for anaemia would be:
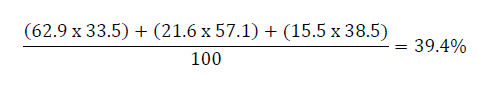
In the above calculation, the percentage of the population that lives in each region is multiplied by the percentage of individuals with anaemia in the same region. These values are added together and divided by 100.
Specific statistical software with the capacity to handle complex survey design should be used to calculate the results. Such programs use weights that have been generated by the analyst and account for the survey design used on the basis of information entered into the software. Applying these design variables, the software can be used to calculate the weighted 95% confidence intervals (CIs) around the estimate and the DEFF.
When it is not possible to perform a survey using PPS sampling of PSUs, for example, if PSUs were selected using a simple random or systematic sampling methodology with a sample of participants interviewed in each cluster, then the population size of each sampled cluster is required to correctly analyse the data. The approach to weighting is similar to that described above, with the difference that the population size in each cluster surveyed would be used to calculate the sample weight.
Calculating sample weights for non-response
If the response of households and individuals is similar (and considered as random) across clusters, then weighting for non-response may not be needed. If the response for a primary outcome of the survey differs dramatically by cluster or stratum, then sampling weights may reduce the potential bias for the national estimates. If weighting for interview non-response for households is considered necessary, this adjustment may need to be repeated for each of the different population groups selected from households in the survey. Household response rates may differ due to such factors as a high proportion of the population in a cluster that works away from home, or in situations where a cluster has a wide range of socioeconomic status (SES). Lower SES households are typically more likely to participate, which may bias results toward a higher prevalence of anaemia and micronutrient deficiencies unless the household weight is adjusted for the higher refusal (non-response rate) among high SES households. Box 15.1 shows an example of how a household non-response weight is calculated. Adjusting for non-response for issues such as SES requires additional information.
Box 15.1. Calculation of sample weights for household non-response at the cluster level
Household sampling weight = HHT ÷ HHA
- Where:
- HHT = The target number of households to be assessed within each cluster
- HHA = The number of households actually assessed within each cluster
Example: 10 households were to be assessed in each cluster (HHT = 10). Between 9 and 10 households were successfully interviewed in all clusters except one, where only 6 households were assessed (HHA = 6). Four households did not respond. The additional household weight for this cluster would be 10 ÷ 6 = 1.667. This can be interpreted as every household assessed in the cluster representing 1.667 households.
For individual response rates, most surveys assess responses separately for interviews and for biological specimen collection. The level of non-response for specimen collection is commonly higher than that for interviews. Where non-response differs significantly between clusters or strata, the sample weight should be adjusted to avoid potential bias of results towards locations with higher response rates. Therefore, in some surveys, for each population group, there may be one sampling weight applied to the questionnaire and another sampling weight used for biological specimens. This may apply at the cluster or the stratum level.
Household or individual sampling weights may also need to be adjusted if specimens are misplaced during transfer to the laboratory for analysis. For example, if samples of salt collected at the household level for later laboratory analysis of iodine content go missing before reaching the laboratory, this must be considered as a non-random non-response and the household sampling weight for the salt iodine analysis results need to be adjusted accordingly.
Statistical analyses for micronutrient surveys
Survey data, descriptive data for the sample population, household characteristics, and micronutrient-related indicators are usually presented as weighted percentages with 95% CIs. Where the data are skewed, meaning they are not normally distributed, then the weighted median or geometric mean is presented, along with 95% CIs where these can be generated. It is crucial to avoid reporting a weighted mean and an unweighted CI.
Box 15.2 provides information about the importance of presenting 95% CIs.
Box 15.2. The 95% confidence interval
It is important to include the 95% CI around any estimate for primary survey outcome indicators, where calculation of this variance is feasible. Surveys present data from a random sample of households or a specific population group that are intended to represent all households or the entire population group in the country. Therefore, all calculations are considered to be estimates of the “true” values for the entire population.
The 95% CI around a prevalence or coverage estimate provides a range of values that includes the “true” estimate, with 95% confidence. Confidence limits are the numbers at the upper and lower end of a confidence interval, and they determine the width of the interval. The width of the CI provides a measure of the precision of the survey estimate: the narrower the confidence limits, the greater the precision.
The scope of this manual does not allow detailed information about statistical tests or the syntax for defining the sample design and the tests themselves. It is recommended that country teams work with statisticians experienced in processing and analysing data from complex surveys. In the interpretation of data, it is critical to remember that sampling errors, measurement errors and the skills of the survey team members all influence the precision of results.
Outcome results tables
Results tables should specify the indicator measured, the population group and age range(s) in which it is being measured, the unweighted sample size, a measure of central tendency (mean, geometric mean or median), precision (95% CI) and/or variability [such as standard deviation (SD) or standard error, interquartile range (IQR) with reported units (for example g/L)] and the prevalence above or below a specified cutoff point, where appropriate. Data should be presented as stratified (by region, age or sex) and as national estimates for the population group. If the data have been adjusted for any other factors (for example inflammation, smoking, or elevation above sea level), this should be noted in a footnote to the table. Table 15.3 shows a sample table layout.
It can also be informative to report data quality check information. Sample table shells are shown for Hb data quality checks in the online tool “Hemoglobin data quality table shells.”
Table 15.3. Sample mean haemoglobin and prevalence of anaemia in children 6–59 months of age
Characteristic Sample size (unweighted) Haemoglobin (g/L) Prevalence of anaemia Mean SD 95% CI % haemoglobin
<110 g/L95% CI Sex Male Female Residence type Urban Rural Strata (region) North region South Region East Region West Region Poverty Poor Non-poor Total (National) Data are weighted to account for survey design
Haemoglobin values are adjusted for elevation above sea level
This table does not include IQRSee Module 3: Biomarker selection and specimen handling for more information on adjustments specific to target groups.
-
Stukel DM. Feed the Future population-based survey sampling guide. Washington (DC): Food and Nutrition Technical Assistance Project, FHI 130; 2018 (https://www.fantaproject.org/sites/default/files/resources/FTF-PBS-Sampling%20Guide-Apr2018.pdf, accessed 19 June 2020). ↩